In einer Raumzeit gibt es eine Zeit- und mehrere Raumdi­men­sio­nen. In der für uns erleb­ba­ren Welt gibt es genau drei Raumdi­men­sio­nen. Nun spricht in der Diffe­ren­ti­al­geo­me­trie nichts dagegen, auch Mannig­fal­tig­kei­ten mit mehre­ren Zeitdi­men­sio­nen zu betrach­ten. In diesem Projekt geht es um algebra­ische Struk­tu­ren, insbe­son­dere die Gruppe SO(p,q), die die Dynami­ken und die Geome­trie von solchen sogenann­ten pseudo-Riemann­schen hyper­bo­li­schen Räumen mit mindes­tens einer Zeitdi­men­sion beschreiben.  

In meinem Promo­ti­ons­pro­jekt beschäf­tige ich mich mit höherer Teich­mül­ler­theo­rie, einem Thema, welches Diffe­ren­ti­al­geo­me­trie mit anderen mathe­ma­ti­schen Berei­chen wie Algebra und Analy­sis verbindet.

Die Grund­lage für diese Theorie ist die Unter­su­chung von zweidi­men­sio­na­len Flächen und von Gruppen die gewisse „schöne“ Dynami­ken auf diesen Flächen beschrei­ben. Von beson­de­rem Inter­esse sind hier Flächen mit hyper­bo­li­scher Struk­tur, was bedeu­tet, dass die Fläche lokal negativ gekrümmt ist, ähnlich wie ein Sattel. Den sogenann­ten Teich­mül­ler­raum kann man dann als Abbil­dun­gen von der Funda­men­tal­gruppe einer Fläche in eine spezi­elle Gruppe, die zu der allge­mei­nen hyper­bo­li­schen Fläche gehört, beschreiben.

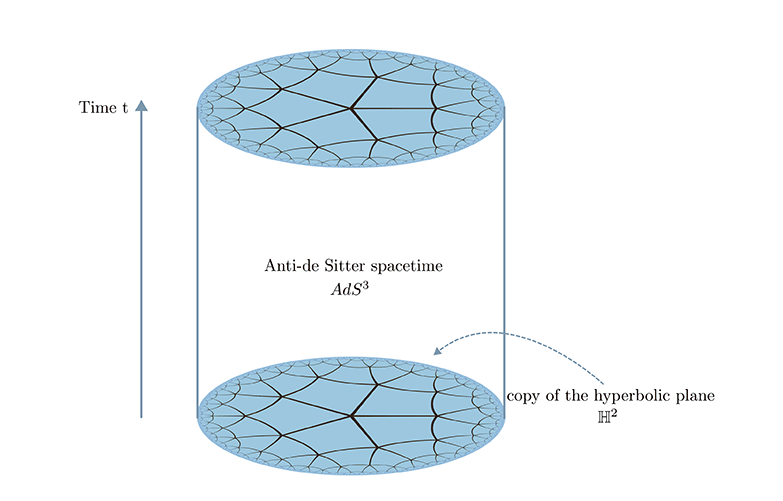
In höherer Teich­mül­ler­theo­rie schauen wir uns ähnli­che Abbil­dun­gen an, aber in Gruppen, die anderen Räumen zugeord­net sind. Während des Projek­tes werde ich mich beson­ders auf pseudo-hyper­bo­li­sche Räume und deren zugehö­ri­gen Gruppen SO(p,q) konzen­trie­ren. Diese Räume kann man sich als Raumzei­ten mit negati­ver Krümmung und mehre­ren Zeit- sowie Raumdi­men­sio­nen vorstel­len. Ein niedrig-dimen­sio­na­les Beispiel für einen solche Raum wäre der Anti-de Sitter Raum, der auch in der Physik, z.B. in der AdS/CFT-Korre­spon­denz eine Rolle spielt.

Konzepte, die in niedri­ge­ren Dimen­sio­nen (für kleine Zahlen p und q) bereits bekannt sind, können verall­ge­mei­nert und weiter unter­sucht werden. Die Erfor­schung dieser höheren Teich­mül­ler­räume kann im Machine Learning auch Anwen­dung durch Graphen­ein­bet­tun­gen finden.