Der Nachweis von Gravi­ta­ti­ons­wel­len (GW) hat ein neues Fenster zum Univer­sum geöff­net, durch das wir die Physik der Verschmel­zung von Schwar­zen Löchern und Neutro­nen­ster­nen studie­ren können. Durch die Analyse von GW können wir auf Eigen­schaf­ten der entspre­chen­den astro­phy­si­ka­li­schen Systeme schlie­ßen. Die derzei­ti­gen Analy­se­me­tho­den sind jedoch rechne­risch zu teuer, um mit der wachsen­den Daten­menge umgehen zu können. Meine Forschung befasst sich daher mit der Entwick­lung effizi­en­ter Metho­den des maschi­nel­len Lernens für die GW-Analyse.

Bei der Verschmel­zung von binären Syste­men aus Schwar­zen Löchern oder Neutro­nen­ster­nen werden Gravi­ta­ti­ons­wel­len (GW) emittiert, die Infor­ma­tio­nen über die Dynamik des Systems enthal­ten. Der Nachweis von GW bietet daher die spannende und einzig­ar­tige Möglich­keit, Einblick in diese Ereig­nisse zu gewin­nen. Die derzei­ti­gen Analy­se­me­tho­den sind jedoch langsam und rechen­in­ten­siv. Dies wird mit zuneh­men­der Dichte der detek­tier­ten Signale aufgrund der konti­nu­ier­li­chen Verbes­se­rung der Detek­tor­emp­find­lich­keit zuneh­mend proble­ma­tisch. Effizi­en­tere Analy­se­me­tho­den sind daher für den Fortschritt in der Gravi­ta­ti­ons­phy­sik unerläss­lich. Meine Forschung befasst sich mit der Entwick­lung von Metho­den des maschi­nel­len Lernens, um die Analyse von GW zu beschleunigen.

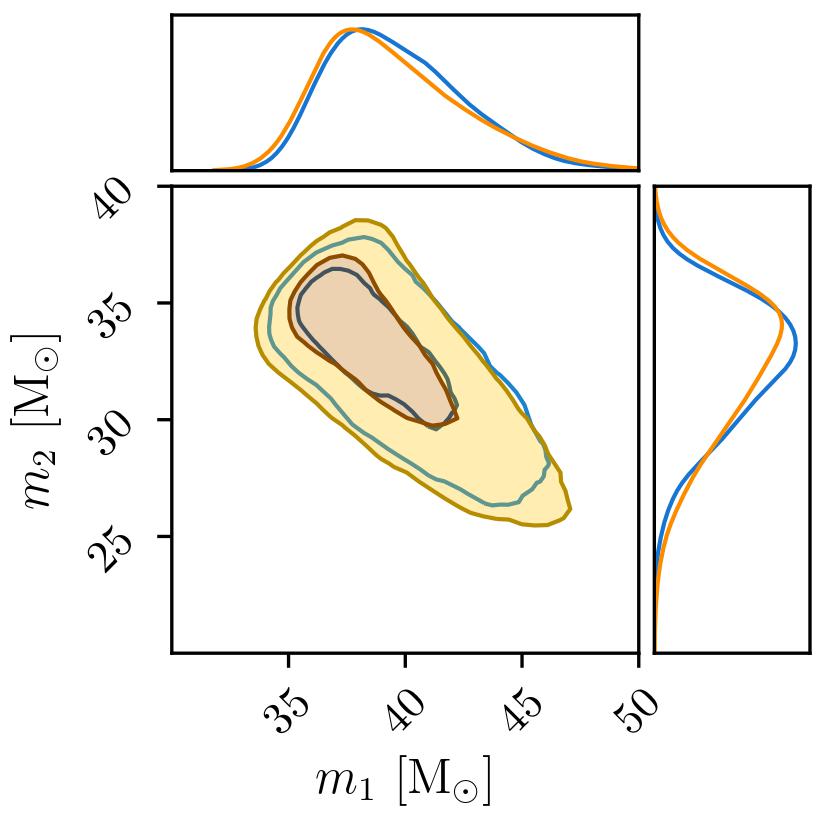
Mein derzei­ti­ger Schwer­punkt liegt auf der Schät­zung der Parame­ter astro­phy­si­ka­li­scher Systeme (z.B. der Massen) anhand der in den Detek­to­ren beobach­te­ten GW-Daten. Diese Aufgabe kann als ein inver­ses Problem inter­pre­tiert werden. In der Vorwärts­rich­tung wird die Wellen­form für gegebene Parame­ter im Rahmen der Allge­mei­nen Relati­vi­täts­theo­rie simuliert. Wir sind an der anderen Richtung inter­es­siert; anhand der gemes­se­nen GW-Daten schät­zen wir die Parame­ter mit Metho­den zur simula­ti­ons­ba­sier­ten Inferenz. Dazu trainie­ren wir ein neuro­na­les Netz, welches die so genannte A‑pos­te­riori-Vertei­lung model­liert. Durch die amorti­sierte Berech­nung für verschie­dene Ereig­nisse und den direk­ten Zugriff auf die gesuchte Wahrschein­lich­keits­dichte ermög­licht unser Ansatz eine schnelle Analyse von GW mit niedri­ger Latenz.