In a space­time we have one time dimen­sion and multi­ple space dimen­sions. In our reality we experi­ence three space-like dimen­sions. Now in differ­en­tial geome­try, nothing keeps us from consid­er­ing manifolds with multi­ple time-like dimen­sions. In this project we study algebraic struc­tures, in partic­u­lar the group SO(p,q), which describe the dynam­ics and the geome­try of so-called pseudo-Riemann­ian hyper­bolic spaces with at least one time dimension.

​

In my project I will study higher rank Teich­müller theory, a topic that connects differ­en­tial geome­try and other mathe­mat­i­cal areas such as algebra and analysis.

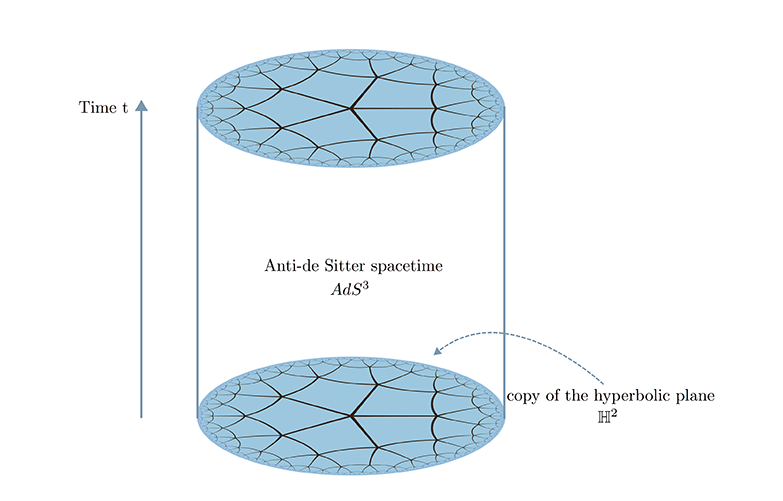
The base for this theory is study­ing two-dimen­sional surfaces and groups that induce certain “nice” dynam­ics on these surfaces. Of partic­u­lar inter­est here are surfaces with a hyper­bolic struc­ture, meaning that the surface locally has a negative curva­ture, similar to the one of a saddle. So-called Teich­müller space then can be described as maps from the funda­men­tal group of a surface into a special group related to the hyper­bolic plane. In higher rank Teich­mueller theory, we look at similar maps but instead consider groups connected to other spaces. During this project I will be partic­u­larly inter­ested in pseudo-hyper­bolic spaces that are connected to the group SO(p,q). These spaces can be thought of as space­times of negative curva­ture with multi­ple timelike direc­tions as well as multi­ple space­like direc­tions. A low-dimen­sional example is the Anti-de Sitter space which plays a role in physics, for example in the AdS/CFT correspondence.

Concepts known in lower dimen­sional cases (for the numbers p and q small) can be gener­al­ized and studied further. The study of these higher rank Teich­mueller spaces could be inter­est­ing as well for machine learn­ing, using graph embeddings.